
По опыту, многие начинающие геймдизайнеры избегают работы с балансом, словно это черная магия или нужно иметь серьезное математическое образование. Специалисты поопытней уже авторитетно заявляют, что математика не нужна.
В первую очередь надо разбираться в самих играх, а потом уже уметь что-то считать. Поэтому я расскажу о работе с балансом без использования математики — на палках урона посмотрим, как уравновесить силу оружия, чем танк отличается от разбойника, и как точки спавна влияют на винрейт.
Статья будет полезна тем, кому надо заняться балансом, но не знает с чего начать, а также начинающим геймдизайнерам, которые будут выбирать специализацию. Ну и всем, кто просто интересуется, чем занимаются ГД, когда не придумывают новые виды лутбоксов.
Не будем слишком глубоко вдаваться в детали конкретных расчетов. В интернете достаточно практических советов: есть цикл статей по балансу на Манжетах ГД, в блоге нашего продюсера Анатолия Шестова есть переведенные лекции Яна Шрайбера. Там можно найти ответы на многие вопросы, если они появятся по ходу чтения. Советую, если не пугают обилие цифр и расчеты.
А я расскажу, куда смотреть и на что обращать внимание. Потому что точность расчетов — дело техники и опыта. Главное начать.
Основа основ
В любой игре со сражениями есть боевые единицы. Юниты в RTS, персонажи в RPG, противники в шутерах. У них есть боевые параметры, которые зависят от целей дизайна: хотим ли мы сделать единицу пушечным мясом, эпическим противником или еще чем-то.
Так как мы говорим о боях, то у юнитов должна быть сила урона. Представим этот урон палкой. Эти палки одноразовые — когда юнит ее использует, она исчезает.

Скорее всего у юнита несколько таких палок. Их количество зависит от того, как долго он живет. Если юнит живет 5 раундов и тратит одну палку за раунд, значит у него 5 палок урона.
Вместе они составляют боевую силу юнита, и если приложить палки друг к другу, получится прямоугольник:

Поэтому первое, что надо запомнить:
Сила юнита = Урон юнита * Время жизни (его HP)
Все остальное мы возьмем из знания игр и здравого смысла. Допустим, прямоугольник на картинке описывает силу некого юнита. Например, Паладина в RPG.
Обычно в ролевых играх гораздо больше параметров, чем HP и урон — есть шансы крита и уворота, дистанция атаки, скорость и так далее. Но так или иначе все эти свойства можно свести к эквиваленту урона или времени жизни. Двойная скорость атаки означает, что за раунд юнит наносит двойной урон, а шанс уворота 50% добавляет юниту столько же времени жизни, как если бы мы вдвое увеличили его HP.
Слишком много математики, вернемся к палкам. У разных юнитов палки урона могут быть разной длины (силы). И время жизни (раунды) тоже бывает разное:

Это типичные классы персонажей в RPG. Воин обычно самый средний. Танк долго живет, но наносит меньше урона. Разбойник — это стеклянная пушка, живет недолго, зато наносит огромный урон.
Но как понять, сбалансированы ли эти классы между собой?? Ответ вы могли уже узнать — надо просто посчитать площади прямоугольников. Если они одинаковые, значит у классов одинаковая сила и они в балансе между собой.
Теперь сделаем нашего танка поинтересней. Подумайте, что это за персонаж:

За этой фигурой скрывается Берсеркер — танк, который получает бонус к урону, когда у него остается мало здоровья. Его сила также равна площади фигуры на рисунке — она считается, как сумма двух прямоугольников.
Первый навык балансера — видеть геймплей за абстракциями. За прямоугольниками, за наборами цифр. Если научиться описывать геймплей в схемах (даже таких примитивных), цифрах и параметрах, это заработает и в обратную сторону — глядя на цифры, начинаешь представлять, как это будет играться.

Баланс снаряжения
В RPG есть не только персонажи, но и снаряжение. Например, мечи. Как посчитать баланс меча? Точно также.
У меча есть некий урон, но нет времени жизни. Меч «живет» столько, сколько игрок захочет им пользоваться, и мы не знаем, сколько это. Ну и ладно. Просто скажем, что меч живет 100% своей жизни.
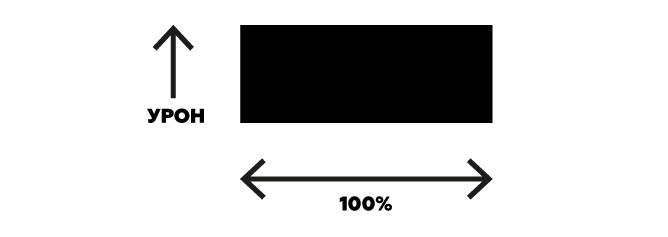
Таким образом, сильнее будет тот меч, у которого больше урон (потому что все мечи живут 100% времени). Но что, если у нас в руках Потрошитель Гоблинов, который наносит им двойной урон? Как понять, насколько он сильнее обычного меча?
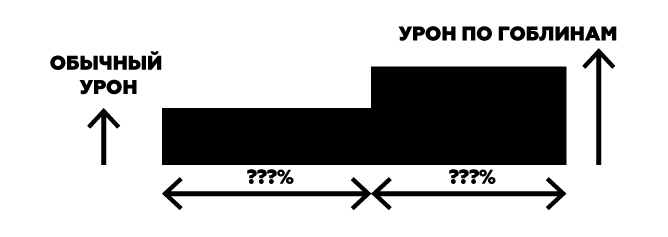
Мы знаем, что меч живет 100% времени, но не знаем, какая часть из этого — обычный урон, а какая — двойной. Это мы легко можем узнать у наших коллег, которые занимаются миссиями/уровнями.
Допустим, треть всех врагов в игре — это гоблины. Значит, одну треть своей жизни меч наносит двойной урон и две трети — обычный. Теперь можем сравнить его с обычным оружием. Стандартный меч имеет 1 урона * 100% = 1 силы. Потрошитель Гоблинов имеет 1 урона * 67% + 2 урона * 33% = 1,33 силы. То есть он на 33% сильнее обычного меча. И если мы захотим сделать его равным по силе обычному мечу, придется просто уменьшить обычный урон Потрошителя Гоблинов.
Ничего сложного. Если вы умеете считать площади прямоугольников — значит вы знаете с чего начать баланс юнитов и снаряжения.
Ситуативный баланс
Достаточно легко сравнить по силе 2 меча. Они работают одинаково, только с разным уроном. А если у нас шутер, автоматы, дробовики и снайперские винтовки? Они по-разному работают, дают разные ощущения и требуют разных стратегий. Их сила зависит от ситуации, в которой вы оказались. Например, дробовик бесполезен на дальней дистанции, а со снайперкой тяжело управиться, когда враг мелькает прямо перед носом.
Если упростить — снайперская винтовка всегда выиграет на дистанции, а дробовик всегда выиграет вблизи. Как узнать равны ли они по силе?
Допустим, в игре всего два вида оружия — дробовики и винтовки. И две карты — лабиринт и коридор. Игрок обязан выбрать оружие до того, как ему выпадет карта.
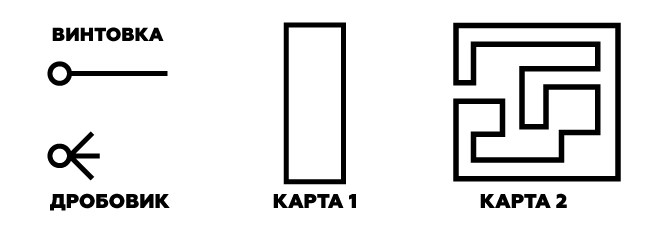
На первой карте сила винтовки равна 100%, а дробовика 0% (винтовка всегда выигрывает). На второй наоборот. Чтобы понять, равны ли они по силе в среднем, нам надо понять, как часто выпадает та или иная карта. Если шанс выпадения каждой карты равен 50%, то оба вида оружия будут равны между собой. В любом случае ваш шанс победить будет 50%.
Если заметили, я упустил часть важных правил — точки появления игроков. Даже если вы играете в коридоре, но появились очень близко друг к другу, дробовик выиграет. Поэтому правила появления игроков тоже надо держать в голове.

А что если мы поменяем правила, и игрок сможет выбирать оружие после того, как узнает тип карты? Тогда он сможет выбрать лучшее на этой карте оружие. В этом случае убедиться в том, что у игрока не будет однозначно самого лучшего выбора — это задача левел-дизайнера. Ему надо сделать так, чтобы на каждой карте было равное количество секций, в которых винтовка или дробовик будут иметь преимущество. Теперь уже от навыка игрока будет зависеть, сможет ли он перетащить стычку туда, где у него преимущество.
Балансер в свою очередь должен представлять структуру карты, понимать, как много секций того или иного типа на карте и вносить соответствующие изменения в силу оружия (как в примере с Потрошителем Гоблинов).
Если в нашей RPG у нас треть врагов были гоблинами, то в шутере нам надо знать сколько процентов от карты составляют коридоры, а сколько — тесные комнаты. Но принцип от этого не поменяется.
Силу оружия можно посчитать таким же образом: умножить урон на процент времени, когда оно обладает преимуществом на карте. Поэтому вполне возможно, что дисбаланс какой-то пушки (слишком сильная или слабая) связан не с настройками, а левел-дизайном.
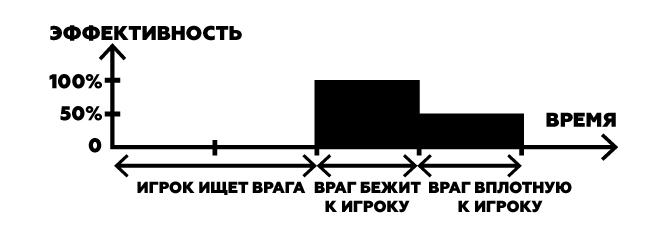
Этот принцип можно распространить дальше. Есть много причин, по которым оружие может считаться бесполезным в определенный момент времени. Возьмем дробовик и проследим за его жизнью:
- Игрок появился на точке спавна. Оружие бесполезно, потому что рядом нет и не может быть врагов.
- Игрок приблизился к центру карты и увидел противника. Противник слишком далеко — дробовик бесполезен.
- Игрок идет на сближение. На средней дистанции можно стрелять, но из-за разброса половина дробин летят мимо. Дробовик полезен лишь наполовину.
- Игрок добрался до противника и стреляет в упор. Максимальная эффективность.
Теперь среднюю силу силу дробовика снова можно посчитать как сумму площадей прямоугольников:
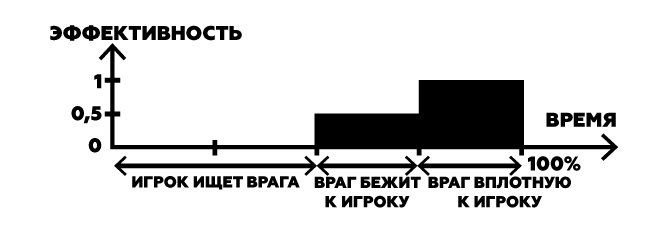
Для другого оружия можно построить еще одну хронологию. Например, со снайперской винтовкой игроку не надо сближаться с противником, надо только встретиться. Поэтому у винтовки максимальная эффективность будет в середине «жизни». И уменьшенная эффективность в конце:
Это намеренно упрощенный пример. Всегда можно посчитать точнее, используя гладкие математические функции, зависящие от дистанции и точности оружия + учитывать больше условий эффективности и зависимостей. Эффективность оружия в какой-то момент может быть равна не 100% или 50%, а 37% или 42. А площадь считать интегралом от этих функций. Но общий принцип от этого не изменится.
Чтобы правильно посчитать баланс, в первую очередь надо знать не математику, а как и по каким правилам работает ваша игра. Понимать, что и в какой момент происходит, как развиваются события. Мы знаем, что на баланс оружия влияет момент его выбора (до того, как известна карта или после), точки спавна, левел-дизайн и развитие матча по ходу игры. Задача посчитать баланс — это задача понять игру.
Предварительные итоги
Мы обсудили баланс отдельных сущностей, персонажа или оружия. Пока что я рассказал про самые основы — с чего начать, когда надо что-то сбалансировать:
- Поставить цели. Потому что расчеты не делаются в вакууме.
- Понять, как работает ваша игра. И какие в ней правила.
- Представить, что происходит в игре в каждый момент времени.
- Определить, как эта ситуация влияет на силу того, что вы хотите сбалансировать.
А в следующей статье я затрону более глобальные вещи, которые связаны со всей игрой: взаимодействие баланса, экономики и прогрессии игрока. Еще будет про динамику развития и влияние фундаментальных правил игры, таких как правила боя.

![]()
Похожие публикации
40 лет адвергейминга — ретроспектива рекламных видеоигр
Минус уши или как не испортить звук в игре с самого начала
Как улучшить геймдизайн с помощью оптимальных стратегий
Комментарии 38

![]()
В хорошей игре тот кто самый дамажный — он же как правило и самый незащищённый.
Это автоматом повышает требования к «прямоте рук», а на самом деле к тому, чтобы ДУМАТЬ быстро и наперёд, и реализовать дамаг -не дохнуть.
Поэтому те, кто взял дамагеров, очень быстро расслоятся на 15% нагибаторов, ещё 20-30% тех кто хочет и учится, и остальную часть «крабов».
В случае WoW и других игр с развитым PvE процент смещён в плюс, т.к. мобов валять проще, чем игроков.
В хорошей игре кроме урона и защиты есть и более интересные способы баланса. Можно сбалансировать разные классы так, что номинально все будут иметь одинаковый DPS и защиту, но играться будут совершенно по-разному. Например:
— медленные сильные удары против слабых но частых.
— точечные удары против сплеш-атак
— урон можно блокировать бронёй, поглощать за счёт здоровья или уклоняться
— бонусы за контратаки, удары с разбега, комбо, классовое оружие и т.д.
— станы, обезоруживание, связывание, отбрасывание, принудительное агро…
И это всё только для для ближнего боя.
То есть само понятие «самый эффективный» в зависимости от ситуации будет сильно меняться, и это не всегда будет «самый дамажный».
Компенсируем это механиками и снаряжением, которые не дают попасть по разбойнику, стримом «разбойник, в которого не возможно попасть даже берсерку», смотрим — затопило ли форум слезами мазилами-берсерками, которые машут своими массивными топорами без шанса на попадание и дохнут от бакстабов с пятерным уроном.
![]()
Статья интересная. Даже появилось желание применить подобный подход в своей игре (от необходимости балансировать которую мне хочется запереться в шкафу без кофе и печенек и громко выть от тоски). Я даже выписывал вопросы и замечания по ходу прочтения (чего обычно не делаю). Вот такие например:
Это типичные классы персонажей в RPG.
Но что, если у нас в руках Потрошитель Гоблинов, который наносит им двойной урон?
В шутере нам надо знать сколько процентов от карты составляют коридоры, а сколько — тесные комнаты
Теперь среднюю силу силу дробовика снова можно посчитать как сумму площадей прямоугольников:
— Товарищ майор, вот вы в академии учили высшую математику. Она вам когда-то в жизни пригодилась?
— Да. Один раз у меня танк в болоте застрял. Я согнул лом интегралом и вытащил.
Просьба не закидывать кирпичами, я ни в коей мере не критикую статью — наоборот, она мне очень понравилась (добавил в избранное, буду перечитывать). Не тем, что учит балансировать игру без математики, а тем, что позволяет понять математику в простой и наглядной форме, показать начинающим гейм-дизайнерам, что в ней нет ничего страшного и сложного. Автор (который, видно, много знает по теме) не отмахивается от новичков со словами «ну вы, это, наймите тестировщиков, они там все потестируют», а честно пытается на пальцах объяснить довольно-таки непростые вещи. Кто знает, может это побудит кого-то пойти подучиться и заняться вычислениями уже всерьез (а значит, научиться «понимать игру», как об этом поэтично сказано в конце статьи).
С нетерпением жду продолжения.
![]()
Спасибо за развернутый комментарий и замечания.
Вы все верно подметили. Материал намеренно упрощен. И даже не чтобы не отпугивать читателей. У материала две основных цели:
— Сломать страх перед подобными задачами у тех, у кого он есть.
— Продемонстрировать, что баланс — это вопрос дизайна. Очень часто можно встретить отношение типа «я придумал штуку, а цифры потом настроим чтобы было хорошо». Как бы отделяя баланс от дизайна и думая, что эти вещи могут работать по отдельности. Такой подход работает только если фундаментальный дизайн в порядке. А если в нем есть проблемы, правки цифр — это как пластырь на перелом. В конце концов, математика — это описательный язык. Нужно знать что ты ею описываешь.
Это не материал с конкретными прикладными советами. В начале я дал ссылку на Яна Шрайбера, я очень люблю его циклы лекций. И говоря совсем честно, мне не кажется что после них мне есть что добавить. Если чувствуете, что вам нужна большая детализация, очень советую почитать их.
Теперь по конкретным моментам.
1) Материал и так получился крупный. Чтобы его еще сильнее не раздувать я решил просто ввести некоторые аксиомы, о которых не полагается задумываться, а нужно просто принять на веру. Думаю, мне надо будет больше внимания уделять тому, что можно просто сказать, а что нужно пояснять.
2) Отсутствие осей в начале прямо вытекает из целей статьи. Я притворяюсь, что тут нет математики, и фокусирую внимание на других вещах. Вероятно, лучшая визуализация «совместно сложенных палок» тут хорошо помогла бы сгладить переход.
3) Говорите все верно. В реальной работе полностью избежать математики не получится. Я просто пытаюсь показать что это не какой-то монстр из интегралов и функций. И в реальных ГД задачах очень редко нужен уровень дальше первого семестра университета, где все еще преподают достаточно базовые вещи. Единственная игра, которая использовала реально сложную математику — третьи герои. Говорят, там баланс считали с помощью дифференциальных уравнений. Все остальное часто можно свести к вот таким простым площадям. Да, если добавить детали, там будут гладкие графики функций, которые считаются интегралами. Но физический смысл интеграла и есть площадь. Я просто сделал функцию достаточно простой, чтобы было наглядней.
Но считать интеграл — это прикладной навык. А идеология та же, что описана в статье.
4) А вот тут я не соглашусь. На своей практике я подобным образом работал с уже существующей игрой. У существующей игры уже есть какая-то модель баланса, даже если она никем никогда не задумывалась. Если цифры просто подгонялись на глаз после множества тестов. В таком случае эту модель надо обнаружить. Это задача reverse engineering, и я такие делал. Возможно выкопать модель баланса из игры, и когда вы ее раскопаете, ее можно будет описать вот подобным образом. Только не так примитивно как я это сделал — вы уже будете знать все детали и зависимости в игре к концу процесса.
На эту тему я опять сошлюсь к Шрайберу, у него есть лекция по реверс инжинирингу баланса стоимости маны в MtG. И она будет очень полезна, даже если работать надо не с ККИ, описанный там подход универсален.
ссылка
Ну и по последнему пункту думаю я дал ответ в начале. Еще раз спасибо 🙂
![]()
На самом деле очень интересно, гейм-дизайн моя мечта, но нелюбовь меня к математикиили нелюбовь математики меня, всегда откладывала эту мечту на самую верхнюю антресоль.
Жаль что в свою бытность школьником IT сфера еще представляла из себя архаичную коллегию магов, нежели столичную академию искусств. Так что надеюсь на продолжение и побегу проверять свои наброски в dnd-модуле 😛.
![]()
Но как понять, сбалансированы ли эти классы между собой?? Ответ вы могли уже узнать — надо просто посчитать площади прямоугольников. Если они одинаковые, значит у классов одинаковая сила и они в балансе между собой.
Смею заявить, что это очень наивный подход к понятию баланса.
![]()
Подход упрощённый, но отнюдь не наивный. Просто здесь рассматриваются лишь две характеристики, в то время как в реальных играх их несколько десятков. Но если каждую из них выразить в численном виде, перемножить между собой (то есть, найти объем многомерного параллелепипеда) и сравнить, то мы как раз и получим, что при равенстве значений (объемов) объекты сбалансированы, а при неравенстве — нет.
![]()
Если решать в лоб, то можно и так. Также можно уменьшать размерность, приводя характеристики к эквивалентам. ХП и броня вместе легко конвертируются в так называемые eHP (эффективные ХП) и сводятся в один параметр. Туда же легко идет уворот и некоторые виды лечения. В свою очередь, скорость атаки и крит достаточно просто конвертируются в урон.
Более неоднозначные параметры тоже можно конвертировать. Преимущество в дистанции атаки (лучник против воина) можно интерпретировать как «несколько бесплатных атак лучника до того как начнется полноценный бой».
![]()
Так или иначе, в конечном итоге всё друг с другом перемножается (подмигивающий смайлик).
Я имел в виду характеристики, которые не сводятся к урону или времени жизни. На ум приходят различные взаимодействия персонажей: бафы, дебафы, хилы и тому подобное. Теперь, когда я думаю об этом, возможны граничные случаи, при которых персонаж вообще не наносит урона, но при этом является «сбалансированной» единицей.
В терминах прямоугольников такие персонажи увеличивают площадь прямоугольников союзников или уменьшают — противников.
Возникает проблема посчитать суммарную силу нескольких юнитов.
![]()
Как только начинается взаимодействие персонажей, происходит комбинаторный взрыв.
Общую силу группы можно представить, как непрерывное количество побежденных монстров (без использования зелий/расходников).
В примере с ценностью тоже не все так просто. Так как ценность ситуативная. Вы вряд ли выберете предмет с «сопротивляемостью к урону вилкой», если ваш следующий противник вооружен пылесосом.
Так же, если большинство противников вооружены вилками, то первый предмет ценнее.
Если разрешить несколько ситуативных модификаторов, то игроки будут вынуждены собирать различные наборы одежды под различные ситуации.
![]()
Так вот откуда берутся эти непомерно дорогие кольца «+10% к вероятности крита». Типа наносим 100 урона в секунду с вероятностью критануть х2 в 10% — так что кольцо дает ажно +20 к урону по мнению геймдизайнера
![]()
Есть нюанс, что крит — параметр относительный. Чем больше у тебя базовой атаки, тем больше дополнительного урона тебе даст крит. А вот цену надо назначить один раз и на всю игру.
Скорее всего, если это кольцо непомерно стоит, то это потому, что его цена считалась относительно ситуации где-то в конце игры. Когда у персонажа уже не 100 урона в секунду, а 1000. И продешевить тут очень опасно, потому что тогда прокачанные персонажи будут поголовно бегать обвешанные критами, куплеными за бесценок.
По этой же причине в мобах на разных этапах игры разные статы экономически выгоднее. В начале матча выгоднее покупать чистый урон. Крит стоит дорого, а ДПСа даст мало. В конце крит покупать выгоднее, потому что он будет давать больше ДПСа, чем урон на те же деньги.
























